در این بخش دو نمونه از تمرین هایی که در درس سیستم های تصمیم یار در بخش برنامه ریزی خطی یا Linear Programming که در سال 89 مطرح شده بود به همراه پاسخ آنها برای یادگیری دانشجویان داده شده است. چند نمونه پرسش دیگر نیز در این تاپیک قابل دریافت است. لطفا اگر در پاسخ ها اشتباهی می بینید تذکر دهید تا تصحیح شود. اگر از این مطلب در جای دیگر استفاده می کنید لطفا لینک به این صفحه را فراموش نکنید.
– مسئله نمونه شماره ۱ از برنامه ریزی خطی ، شرکت تولید ماشین حساب:
یک شرکت تولید کننده ماشین حساب دو نوع ماشین حساب تولید میکند، ماشین حساب علمی و نموداری (گرافیکی). پیش بینی های دراز مدت نشان می دهد که حداقل باید 100 ماشین حساب علمی و 80 ماشین حساب نموداری در روز تولید شود. به دلیل محدودیت در ظرفیت تولید، بیش از 200 ماشین حساب علمی و 170 نموداری نمیتوان در روز تولید کرد. برای راضی نگهداشتن و عمل به قراردادهای بخش حمل و نقل حداقل 200 ماشین حساب بایستی در روز بارگیری و منتقل شود. اگر فروش هر یک از ماشین حسابهای علمی منجر به از دست دادن 2 دلار اما فروش هر ماشین حساب نموداری منجر به 5 دلار سود شود چه تعداد از هرکدام بایستی روزانه ساخته شود تا بیشترین سود خالص را داشته باشیم؟
پاسخ: این سوال در واقع تعداد بهینه ماشین حسابهای تولیدی را میخواهد بنابراین دو متغیر خواهیم داشت:
X: تعداد ماشین حسابهای علمی
Y: تعداد ماشین حسابهای نموداری
به دلیل اینکه تعداد ماشین حسابها نمیتواند منفی باشد پس این دو فرض را در نظر میگیریم:
x > 0 و y > 0
اما در این مسئله باید x > 100 و y > 80 باشد. و همچنین تعداد ماکزیموم نیز تعیین شده است: x < 200 و y < 170
از نظر حمل و نقل نیز داریم: x + y > 200 یا به عبارتی y > –x + 200
و نسبت سود و زیان نیز معادله ما خواهد بود. یعنی:
R = –2x + 5y,
مشروط به اینکه:
100 < x < 200
80 < y < 170
y > –x + 200
ناحیه امکانپذیری:
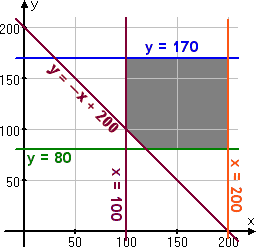
با بررسی رئوس این ناحیه یعنی نقاط (100, 170), (200, 170), (200, 80), (120, 80), و (100, 100), و تست آنها در معادله R مشاهده میکنیم که حداکثر میزان R در نقطه (x, y) = (100, 170) و R=650 خواهد بود. و این جواب مسئله است. 100 ماشین حساب علمی و 170 ماشین حساب نموداری.
– مسئله نمونه شماره ۲ از برنامه ریزی خطی ، سرمایه گذاری در سه محل:
فرض کنید شما 12000 دلار برای سرمایه گذاری در اختیار دارید و سه محل نیز برای سرمایه گذاری وجود دارد. صندوق اوراق قرضه شهری بازگشت سود 7 ٪، اوراق مشارکت بانکی با سود 8٪، و یک حساب با ریسک بالا که انتظار میرود 12٪ سود داشته باشد. برای به حداقل رساندن ریسک شما تصمیم میگیرید بیشتر از 2000 دلار در حساب با ریسک بالا سرمایه گذاری نکنید. بنا به دلایل مالیاتی، شما نیاز به حداقل سه بار سرمایه گذاری در اوراق قرضه شهری دارید. فرض کنید که پایان سال به نحو مطلوبی در حال به اتمام رسیدن است. بهترین حالت سرمایه گذاری چه خواهد بود؟
مجهولات معادله عبارتند از:
X: سرمایه گذاری اوراق قرضه (مضرب هزار دلار)
Y: خرید اوراق مشارکت بانکی (مضرب هزار دلار)
و برای سومین محل سرمایه گذاری باید از این عبارت استفاده کنیم: “چه مقدار پول باقی مانده است؟”
12 – x – y: میزان سرمایه گذاری با ریسک بالا (مضرب هزار دلار)
ضمنا مقدار هیچ یک از سرمایه گذاریها نمیتواند منفی باشد:
x > 0 and y > 0 and 12 – x – y > 0 ⇒ y < –x + 12
همچنین قرار شد که سرمایه گذاری با ریسک بالا بیشتر از 2000 دلار نباشد. یعنی:
(12 – x – y) < 2 ⇒ y > –x + 10
این شرط نیز از شرایط مالیات نتیجه گیری میشود: y < ( 1/3 )x
در نتیجه معادله بهینه عبارت خواهد بود از جمع کل سرمایه گذاریها:
Y = 0.07x + 0.08y + 0.12(12 – x – y) = 1.44 – 0.05x – 0.04y
و به عبارتی:
Maximize Y = 1.44 – 0.05x – 0.04y,
با شرط:
x > 0
y > 0
y > –x + 10
y < –x + 12
y < ( 1/3 )x
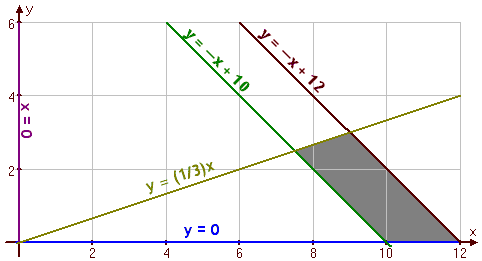
با تست نقاط گوشه یعنی (9, 3), (12, 0), (10, 0), و (7.5, 2.5) به مقدار حداکثر 965 دلار سود خواهیم رسید که از سرمایه گذاری 7500 دلار در اوراق قرضه شهری، 2500 دلار اوراق مشارکت بانکی و 2000 دلار در سرمایه گذاری پرخطر به دست می آید.
استفاده از این نوشتار در صورت نوشتن منبع و لینک به آن آزاد است.

سلام اگه ما بخوایم برای یک محصول برنامه ریزی کنیم اونم در حد انبوه چه کار باید کنیم
سوالتان واضح نیست. به انجمن دانشجویان دانشکده هم مراجعه کنید فکر کنم مثالها و آموزشهای بیشتری وجود داشته باشد.
http://forums.svus.ir